- A fractal is a mathematical shape whose structures repeat indefinitely as you zoom in deeper and deeper.
- In our Universe, many of the structures we see on small scales also show up repeatedly, on larger scales.
- Is it possible that we live in a fractal Universe, and that this continues all the way up and all the way down?
In Big Think
If you take a look at the structures that form in the Universe, many of the things we see on large scales appears at smaller scales, too. The dark matter halos that form around the largest bound structures we know of appear identical to the ones that form around Milky Way-sized galaxies, as well as the tiny substructure clumps that exist both around smaller galaxies and in intergalactic space itself. On the largest scales in the Universe, gravitation is the only force that matters. Under many circumstances, if you wait long enough, gravitational collapse will produce identical structures, just scaled up or down in size depending on the size of your system.
The idea that, if you zoom in far enough, you’ll eventually encounter a structure that repeats the initial pattern you saw on larger scales, is mathematically realized in the concept of a fractal. When similar patterns repeatedly emerge at smaller and smaller scales, we can analyze them mathematically and see if they have the same statistical characteristics as the larger structures; if they do, it’s fractal-like in nature. So, is the Universe itself a fractal?
The answer appears to be almost, but not quite. Here’s the science behind why.

Mathematically, most of us are used to real numbers: numbers that can be expressed in a decimal format, even if that decimal is infinitely long and even if it never repeats. But there are more numbers that mathematically exist than just the real ones; for example, there are complex numbers. Complex numbers have a real part but also an imaginary part, which is a real number multiplied by i, which is defined as the square root of -1. They include the real numbers, but take us beyond the limitations of working with the real numbers alone.
The most famous fractal is the Mandelbrot set, which is illustrated (in the complex plane, where the x-axis is real and the y-axis is imaginary) in the diagram above and the video below. The way the Mandelbrot set works is you consider every possible complex number, n, and then you look at the following sequence:
- n,
- n² + n,
- (n² + n)² + n,
- ((n² + n)² + n)² + n,
and so on. Each new term is the prior term, squared, plus n. If this sequence doesn’t diverge, going to either positive or negative infinity, then your value of n is a member of the Mandelbrot set.https://www.youtube.com/embed/b005iHf8Z3g?feature=oembed
The way the Mandelbrot set is visualized is by representing the border between what’s actually in the set versus what’s outside of it, with color coding showing how far away something is from being a member of the set. (Brighter colors are closer to being in it.) As you can see, many of the patterns that emerge are intricate and self-repeating.
When you see a small region that has truly identical properties to the entire set itself, we call those regions “self-similar.” If something has almost the same properties as the larger set but with subtle differences, it exhibits quasi-self-similarity, but if the small region has truly identical properties to a larger region, then it exhibits true self-similarity.
In the Mandelbrot set, you can identify many regions that show both quasi-self-similarity (which is more common) and true self-similarity (which is less common, but still exists). We’ve mathematically demonstrated this on scales spanning hundreds of orders of magnitude, which is far larger than the physical scales that take us from the smallest subatomic distances to the entire observable Universe.
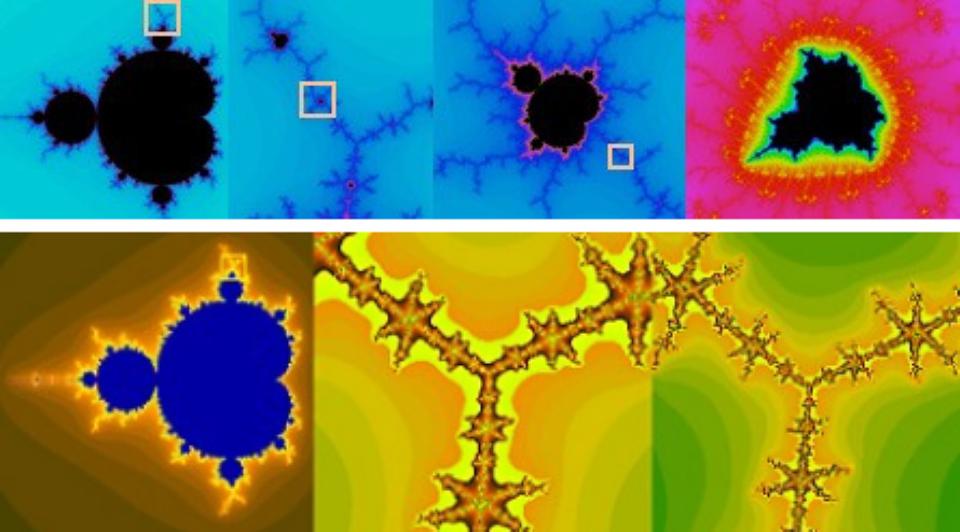
From a mathematical perspective, you can clearly see that if the same rules and conditions apply at all scales, then dependent on what those rules are, you might wind up with a self-similar structure to the Universe, where what appears on large scales also appears on small scales. This was a question of particular interest in the late 20th century, when we had realized two facts in tandem about the cosmos.
- The Universe, as a whole, appears to have a large amount of unseen, invisible mass to it: what we know today as dark matter.
- The overall spatial curvature of the Universe is consistent with being flat, meaning that if you add up all the forms of energy present in the Universe, they equal the critical density, determining the expansion rate (among other things).
In physics, astrophysics, and cosmology, we know we can’t adequately simulate the entire Universe to arbitrary precision. What we can do, instead, is make some simplifying assumptions, and then simulate the Universe to the best of our abilities under that very set of assumptions. One of the more interesting things that we started to do was to run simulations of dark matter in the Universe on a variety of scales. Perhaps surprisingly, they all yielded practically identical results.

When you start with a Universe uniformly full of dark matter, the same gravitational physics is always at play. No matter how uniform you make it, there will always be tiny imperfections: an atom or molecule that isn’t perfectly distributed, a tiny attractive or repulsive force on a subatomic particle, quantum jitter, etc. As soon as your system isn’t perfectly uniform any longer — and perfect uniformity is unstable under the laws of gravity — the overdense regions are going to preferentially attract more matter than the surrounding regions, while the underdense regions are preferentially going to give their matter up to the surrounding regions.
If you start with just a single overdense clump, and you allow it to evolve for long enough (so that every particle in your simulation can complete many complete orbits of whatever trajectory it’s on), you’re going to get a large dark matter halo: spheroidal, diffuse, and with its highest density in the center.
What’s remarkable is that, even if you wildly vary your assumptions, you almost always get the same density profile: getting denser at a specific rate until a certain “turnover radius,” then getting denser at a slower rate until you reach the center.
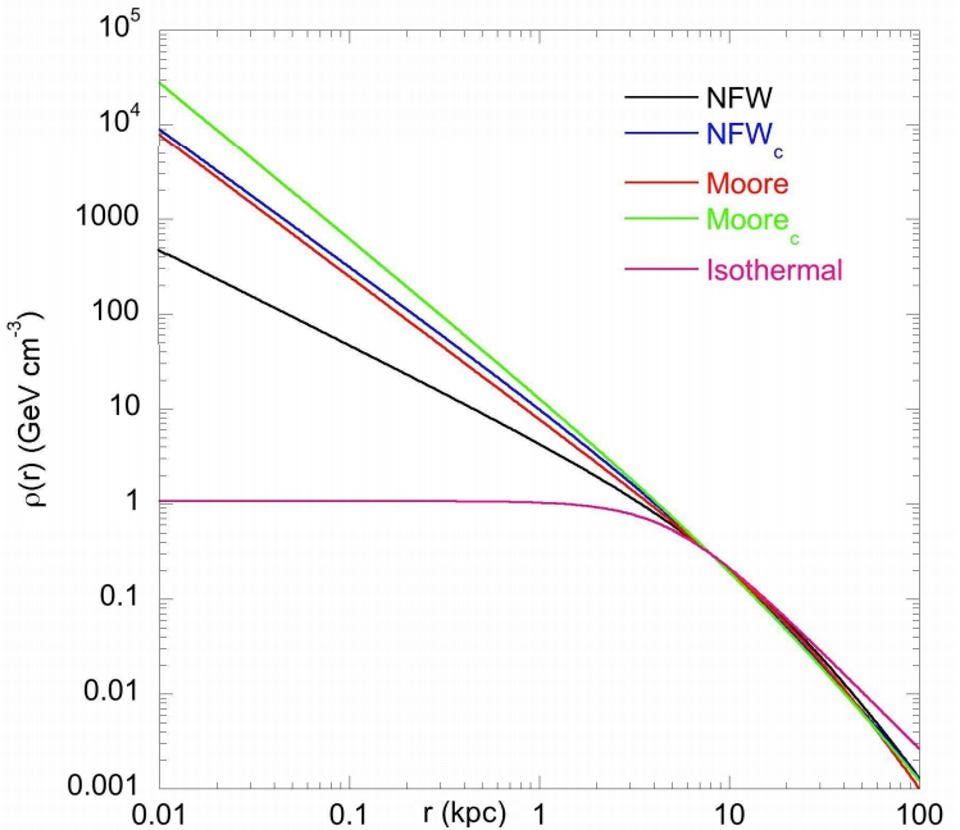
The idea of a universal profile for dark matter halos is one of the most exciting predictions in all of self-similarity in cosmology. What we need to do, however, if we want to be more accurate, is to go beyond a single, isolated system, and instead simulate what’s going on in a more realistic scenario: dark matter in a Universe that’s both expanding and filled with a variety of initial underdensities and overdensities. This, after all, is consistent with what we know and observe about the Universe, and if we’re going to make assumptions, we may as well assume something as close to the actual Universe as possible.
So we run our cosmological simulations, and what we find is the following:
- we produce a great cosmic web,
- where small scales collapse first, as soon as gravity has time to send its influential signal from one overdense region to the surrounding matter,
- where larger scales collapse later, with smaller scale structure superimposed atop it,
- and that as more and more time goes on, even larger scales follow suit, giving rise to a completely self-similar Universe.
In this scenario, you get mini-halos inside regular halos inside giant halos, all connected by filaments that themselves, given enough time and the right properties, will produce their own halos as well, while an even grander web forms on larger scales.

At least, that’s how it would work if we inhabited what’s known as an Einstein-de Sitter Universe: where the only thing making up the Universe is matter, and we have enough matter to reach the critical density, where the amount of “stuff” exactly balances the initial expansion rate. In this toy model of the Universe, the infinite-range gravitational force propagates outward at the speed of light (which is equal to the speed of gravity), and there’s no limit to how large or small a scale can get; you’ll still form the same structures.
But our Universe fundamentally differs from this scenario in three important ways.
1.) We don’t just have one type of matter, but two: normal and dark matter. While dark matter behaves in this self-similar fashion, normal matter is limited. It collides, forms bound structures, heats up, and even triggers nuclear fusion. Once you reach the small scales on which this occurs, self-similarity ends. The feedback interactions between the normal matter and the dark matter will alter the density profiles of the halos in ways that are not easy to figure out. In fact, this remains an open area of study in dark matter research today.

2.) Matter is joined by radiation, an incredibly important component of the Universe. Radiation, because it has an energy that depends on its wavelength, was actually more important in the early Universe. When the Universe expands, it gets less dense; the number of particles (normal matter, dark matter, and photons) remains the same, while the volume increases. But as the Universe expands, the wavelength of the radiation in it also redshifts, becoming lower in energy. The radiation was more important early on, and gets less important as time goes on.
This means, for the first few hundred thousand years of the Universe (and especially in the first ~10,000 or so), the matter overdensities struggle to grow, as the radiation works to effectively wash them out. There’s a lower limit to the scales at which the Universe is self-similar even at early times: your smallest scale structures are going to have at least ~100,000 solar masses in them, which is approximately the masses of globular clusters and the smallest known dwarf galaxies. Below that, the only structures you get are formed from messy collisions and interactions between various normal matter-based structures.

3.) Our Universe is also made extensively of dark energy, which dominates the energy content of the Universe today. If the Universe kept expanding while gravitating, and if the expansion itself wasn’t accelerating, there would be no upper limit to how large these cosmically self-similar structures could be. But because dark energy exists, it basically sets an upper limit to the size of these structures in the Universe: roughly a few billion light-years across.
That might sound enormous, but in an observable Universe that extends for ~46 billion light-years in all directions, even a structure that was 10 billion light-years in all three dimensions — a value much larger than the largest known structure in the Universe, by the way — would occupy only ~1% of the volume of the Universe. We simply don’t have structures that large and never will.
When you take all of this together, it helps us realize a true but perhaps counterintuitive fact about the Universe: on both the smallest and largest cosmic scales, the Universe is not fractal-like at all, and that only the intermediate scales have any chance at exhibiting fractal-like behavior.
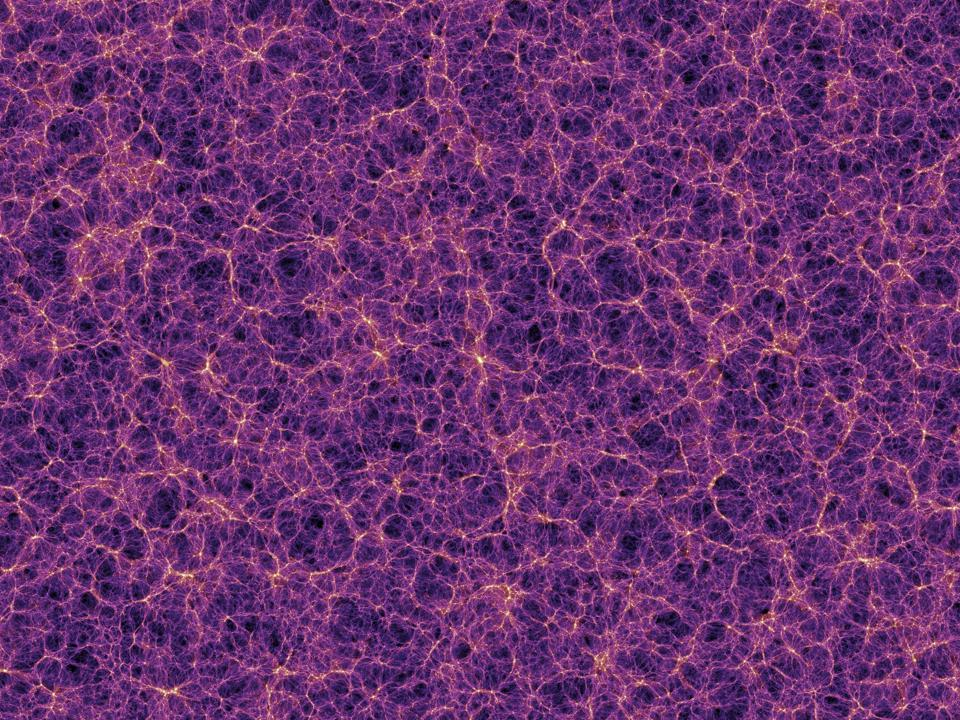
Still, this itself is a rich field of study. People have been working to measure the fractal dimension of the Universe for more than three decades now, attempting to decipher whether it can be well described by one simple fractal parameter or whether multiple ones are required. The nearby Universe is not a good place to measure this, as dark energy has already reared its head for the past 6 billion years.
But if we look at objects that are at a redshift of ~2 or greater, we’re looking back in time to an era where dark energy was insignificant: the perfect laboratory for studying just what type of self-similar properties the Universe had. With a new generation of ground-based and space-based observatories coming online over the next few years, we’ll finally get the comparison between theory and observation that we’ve always wanted. The Universe isn’t a true fractal, but even in the realms where it’s only approximately a fractal, there are still some compelling cosmic lessons just waiting to be learned.
